Usage¶

from sympy2c import symbols, Function, Module
import numpy as np

r, h = symbols("r h")

module_decl = Module()
f = Function("volume_cylinder", h * np.pi * r ** 2, r, h)
module_decl.add(f)

imported_module = module_decl.compile_and_load()
print(
  "the volume of a cylinder of radius 1 and height 2 is",
  imported_module.volume_cylinder(1.0, 2.0))
)

from sympy2c import symbols, Function, Integral, Module
import numpy as np

t = symbols("t")

integral = Integral(exp(-(t ** 2)), t, -oo, oo)
module_decl.add(Function("gauss", integral))

imported_module = module_decl.compile_and_load()
gauss_integral = imported_module.gauss()
print(
  "the numerical error is", abs(gauss_integral - np.sqrt(np.pi)
)

from sympy2c import (symbols, Function,
                     InterpolationFunction1D, Module)
import numpy as np

t = symbols("t")
cos_approx = InterpolationFunction1D("cos_approx")
module_decl.add(Function("f", cos_approx(t ** 2), t))

imported_module = module_decl.compile_and_load()

xi = np.linspace(0, 1.0, 11)
imported_module.set_cos_approx_values(xi, np.cos(xi))
print(
     "interpolation error at x=5 is",
     abs(imported_module.f(0.5) - np.cos(0.5 ** 2))
)

import numpy as np
from sympy_to_c import Module, OdeFast, symbols

y1, y2, y3, t = symbols("y1 y2 y3 t")
k1, k2, k3 = 1e-4, 3e7, 1e4
y1dot = -k1 * y1 + k3 * y2 * y3
y2dot = k1 * y1 - k2 * y2 - k3 * y2 * y3
y3dot = k2 * y2 ** 2

module_decl = Module()
lhs = [y1, y2, y3]
rhs = [y1dot, y2dot, y3dot]
module_decl.add(OdeFast("robertson", t, lhs, rhs))
imported_module = module_decl.compile_and_load()

y_start = np.array([1.0, 0.0, 0.0])
tvec = 0.4 * 10 ** np.arange(0, 6)
rtol = 1e-6
atol = np.array([1e-8, 1e-8, 1e-10])

result, diagnostics = imported_module.solve_fast_robertson(
    y_start, tvec, rtol=rtol, atol=atol
)
print(result)

import matplotlib.pyplot as plt
import numpy as np

from sympy2c import Globals, Module, OdeFast, symbols

p1x, p2x, p1y, p2y, v1x, v2x, v1y, v2y, t, m1, m2 = symbols(
    "p1x p2x p1y p2y v1x v2x v1y v2y t m1 m2"
)

p1x_dot = v1x
p1y_dot = v1y

p2x_dot = v2x
p2y_dot = v2y

d2 = ((p1x - p2x) ** 2 + (p1y - p2y) ** 2) ** 0.5

v1x_dot = -m2 * (p1x - p2x) / d2 ** 3
v1y_dot = -m2 * (p1y - p2y) / d2 ** 3

v2x_dot = -m1 * (p2x - p1x) / d2 ** 3
v2y_dot = -m1 * (p2y - p1y) / d2 ** 3

lhs = [p1x, p1y, p2x, p2y, v1x, v1y, v2x, v2y]
rhs = [p1x_dot, p1y_dot, p2x_dot, p2y_dot, v1x_dot, v1y_dot, v2x_dot, v2y_dot]

module_decl = Module()
module_decl.add(Globals(m1, m2))
module_decl.add(OdeFast("planets", t, lhs, rhs))
imported_module = module_decl.compile_and_load()

imported_module.globals.m1 = 2
imported_module.globals.m2 = 1

p1 = (5, 0)
v1 = (0.2, -0.2)

p2 = (10, 0)
v2 = (0, 0.5)

t = np.linspace(0, 60, 1000)

y, meta = imported_module.solve_fast_planets(
    np.array((p1[0], p1[1], p2[0], p2[1], v1[0], v1[1], v2[0], v2[1]), dtype=float),
    t,
    1e-5,
    1e-5,
)

p1x, p1y, p2x, p2y, v1x, v1y, v2x, v2y = y.T

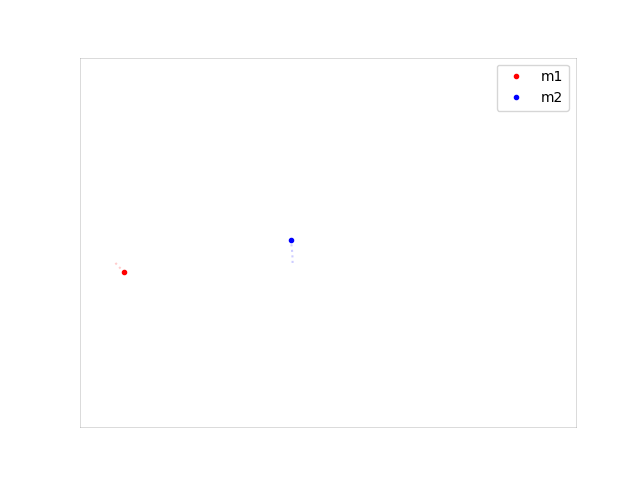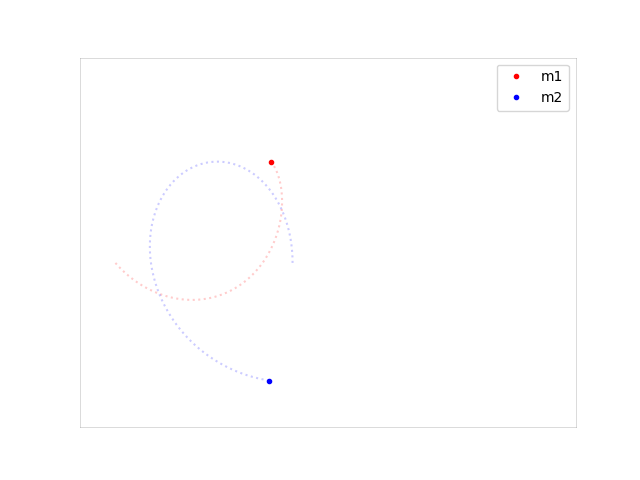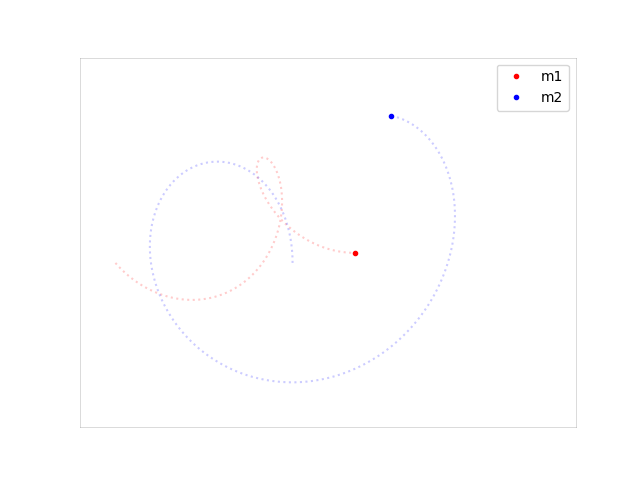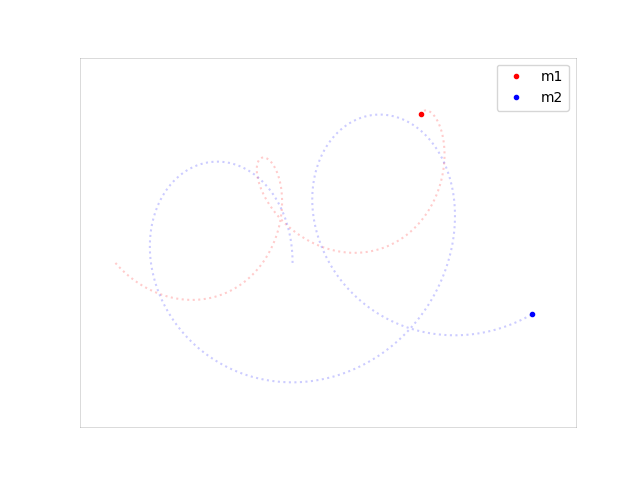
plt.plot(p1x, p1y, label="m1")
plt.plot(p2x, p2y, label="m2")

plt.legend()
plt.savefig("planets.png")